Page 289 - DMTH404_STATISTICS

Unit 21: Confidence Intervals

that Notes

  b (X   ) a  
1
P  n   n   


  S S S  
X  
It is known that ~ t n 1 . We can choose pairs of values (a, b) using a students t-distribution

S/ n
with (n – 1) degrees of freedom such
  b n X   a n  
P      1  

  S Sb/ n S  
In particular, an intuitively reasonable choice is a = b = c say. Then

c n
 t n 1, /2


S

and (X (S/ n)t ,X (S/ n)t ) is 1 –  level confidence interval for . The length of


n 1, /2 n 1, /2


the interval is (2S/ n)t , which is no longer constant.
n-1, /2

Therefore, in this case one cannot choose n to get a fixed length confidence interval of level
1 – . The expected length is, however,
2 2 2  (n/2)
t n 1, /2 Es(S)  t n 1, /2 
n   n   n 1 (n 1)/2)



which can be made as small as we want by making a proper choice of n for a given  and .
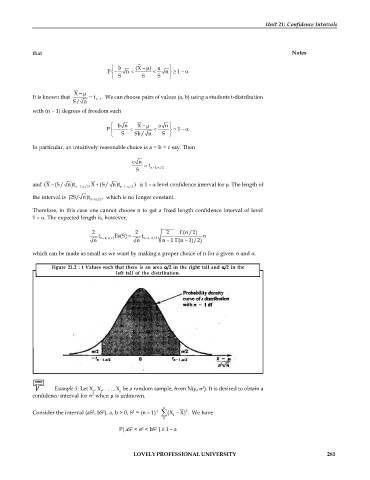
Figure 21.2 : t Values such that there is an area /2 in the right tall and /2 in the
left tall of the distribution.

Example 5: Let X , X , . . . , X be a random sample, from N(,  ). It is desired to obtain a
2
1 2 n
confidence interval for  when  is unknown.
2
n
2
2
2
-1
Consider the interval (aS , bS ), a, b > 0, S = (n – 1)  (X  X) . We have
2
i
1
2
2
2
P{ aS <  < bS }  1 – a
LOVELY PROFESSIONAL UNIVERSITY 281