Page 157 - DCAP601_SIMULATION_AND_MODELING

Unit 9: Simulation of a PERT Network (I)

The square root VT gives us the standard deviation of the project length. Thus, ST=Ö 25=5. The Notes
higher the standard deviation, the greater the ambiguity that the project will be completed on
the due date.
Though the t ’s are randomly distributed, the average or expected project length Te approximately
e
follows a Normal Distribution.
As we have a lot of information about a Normal Distribution, we can make several statistically
significant conclusions from these calculations.
A random variable drawn from a Normal Distribution has 0.68 probability of falling within one
standard deviation of the distribution average. Consequently, there is a 68% chance that the
actual project duration will be within one standard deviation, ST of the estimated average
length of the project, t .
e
In our case, the t = (12+16) = 28 weeks and the ST = 5 weeks. Assuming t to be normally
e e
distributed, we can state that there is a probability of 0.68 that the project will be completed
within 28 ± 5 weeks, which is to say, between 23 and 33 weeks.

Notes It is known that just over 95% (.954) of the area under a Normal Distribution falls
within two standard deviations, we can state that the probability that the project will be
completed within 28 ± 10 is very high at 0.95.

9.2.6 Probability of Project Completion by Due Date

Now, even though the project is estimated to be completed within 28 weeks (t =28) our Project
e
Director would like to know what is the probability that the project might be completed within
25 weeks (i.e. Due Date or D=25).
For this calculation, we use the formula for calculating Z, the number of standard deviations that
D is away from t .
e
D t 25 28  3


Z  e     0.6
S 5 5
t
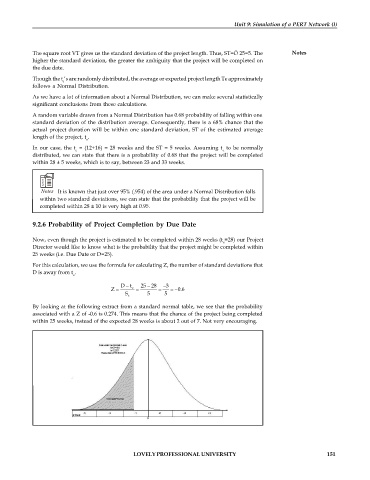
By looking at the following extract from a standard normal table, we see that the probability
associated with a Z of -0.6 is 0.274. This means that the chance of the project being completed
within 25 weeks, instead of the expected 28 weeks is about 2 out of 7. Not very encouraging.

LOVELY PROFESSIONAL UNIVERSITY 151