Page 107 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 7: Mean Deviation and Standard Deviation

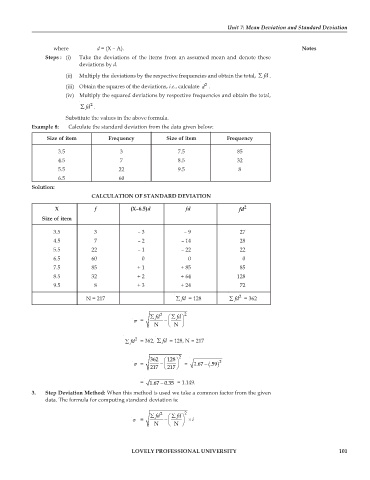
where d = (X – A). Notes
Steps : (i) Take the deviations of the items from an assumed mean and denote these
deviations by d.
(ii) Multiply the deviations by the respective frequencies and obtain the total, ∑ fd .
2
(iii) Obtain the squares of the deviations, i.e., calculate d .
(iv) Multiply the squared deviations by respective frequencies and obtain the total,
2
∑ fd .
Substitute the values in the above formula.
Example 8: Calculate the standard deviation from the data given below:
Size of item Frequency Size of item Frequency

3.5 3 7.5 85
4.5 7 8.5 32
5.5 22 9.5 8
6.5 60
Solution:
CALCULATION OF STANDARD DEVIATION
X f (X–6.5)d fd fd 2
Size of item

3.5 3 – 3 – 9 27
4.5 7 – 2 – 14 28
5.5 22 – 1 – 22 22
6.5 60 0 0 0
7.5 85 + 1 + 85 85
8.5 32 + 2 + 64 128
9.5 8 + 3 + 24 72

2
N = 217 ∑ fd = 128 ∑ fd = 362
∑ 2 ⎛ ∑ fd fd ⎞ 2
σ = − ⎜ ⎟
⎝ N ⎠ N
2
∑ fd = 362, ∑ fd = 128, N = 217

⎛ 362 ⎞ 128 2
σ = − ⎜ ⎟ = 1.67 ( − ).59 2
⎝ 217 ⎠ 217
−
= 1.67 0.35 = 1.149.
3. Step Deviation Method: When this method is used we take a common factor from the given
data. The formula for computing standard deviation is:

∑ fd 2 ⎛ ∑ fd ⎞ 2
σ = − ⎜ ⎟ i ×
N ⎝ N ⎠

LOVELY PROFESSIONAL UNIVERSITY 101