Page 108 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

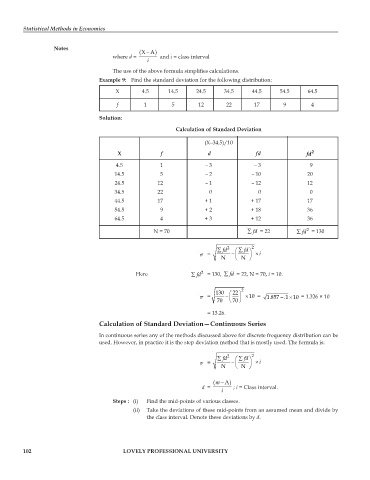
Notes ( XA ) −
where d = and i = class interval
i
The use of the above formula simplifies calculations.
Example 9: Find the standard deviation for the following distribution:
X 4.5 14.5 24.5 34.5 44.5 54.5 64.5

f 1 5 12 22 17 9 4

Solution:
Calculation of Standard Deviation

(X–34.5)/10
X f d fd fd 2
4.5 1 – 3 – 3 9
14.5 5 – 2 – 10 20
24.5 12 – 1 – 12 12
34.5 22 0 0 0
44.5 17 + 1 + 17 17
54.5 9 + 2 + 18 36
64.5 4 + 3 + 12 36

2
N = 70 ∑ fd = 22 ∑ fd = 130

∑ fd 2 ⎛ ∑ fd ⎞ 2
σ = − ⎜ ⎟ i ×
N ⎝ N ⎠

Here ∑ fd 2 = 130, ∑ fd = 22, N = 70, i = 10.

130 ⎛ ⎞ 22 2
σ = − ⎜ ⎟ × 10 = 1.857 .1 10 = 1.326 × 10
×
−
⎝ 70 ⎠ 70
= 13.26.
Calculation of Standard Deviation—Continuous Series
In continuous series any of the methods discussed above for discrete frequency distribution can be
used. However, in practice it is the step deviation method that is mostly used. The formula is:

∑ fd 2 ⎛ ∑ fd ⎞ 2
σ = − ⎜ ⎟ i ×
N ⎝ N ⎠

( − A )m
d = ; i = Class interval.
i
Steps : (i) Find the mid-points of various classes.
(ii) Take the deviations of these mid-points from an assumed mean and divide by
the class interval. Denote these deviations by d.

102 LOVELY PROFESSIONAL UNIVERSITY