Page 307 - DMTH404_STATISTICS

Unit 22: Correlation

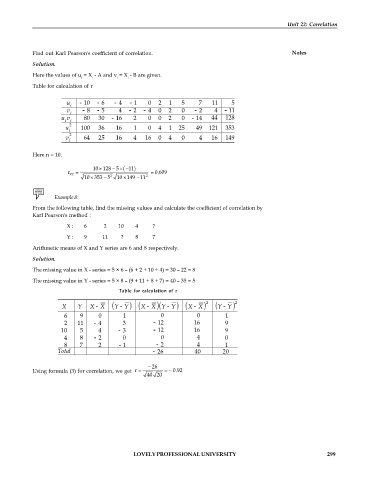
Find out Karl Pearson's coefficient of correlation. Notes

Solution.
Here the values of u = X - A and v = X - B are given.
i i i i
Table for calculation of r

u - 10 - 6 - 4 - 1 0 2 1 5 7 11 5
i
v - 8 - 5 4 - 2 - 4 0 2 0 - 2 4 - 11
i
u v 80 30 - 16 2 0 0 2 0 - 14 44 128
i i
2
u 100 36 16 1 0 4 1 25 49 121 353
i
2
v 64 25 16 4 16 0 4 0 4 16 149
i
Here n = 10.

10 128 5  11 

r XY   0.609
10 353 5 2 10 149 11 2




Example 8:
From the following table, find the missing values and calculate the coefficient of correlation by
Karl Pearson's method :
X : 6 2 10 4 ?
Y : 9 11 ? 8 7

Arithmetic means of X and Y series are 6 and 8 respectively.
Solution.
The missing value in X - series = 5 × 6 – (6 + 2 + 10 + 4) = 30 – 22 = 8

The missing value in Y - series = 5 × 8 – (9 + 11 + 8 + 7) = 40 – 35 = 5
Table for calculation of r
X - X d Y - Yi d X - Xi Y - Yi d X - Xi d Y - Yi 2
d
2
X Y
6 9 0 1 0 0 1
2 11 - 4 3 - 12 16 9
10 5 4 - 3 - 12 16 9
4 8 - 2 0 0 4 0
8 7 2 - 1 - 2 4 1
Total - 26 40 20

 26
Using formula (3) for correlation, we get r    0.92
40 20

LOVELY PROFESSIONAL UNIVERSITY 299